Mapping Multiple LSTM Models on FPGAs

This paper introduces a framework for accelerating multiple Long Short-Term Memory (LSTM) models onto FPGA devices.

Abstract

Recurrent Neural Networks (RNNs) and their more recent variant Long Short-Term Memory (LSTM) are utilised in a number of modern applications like Natural Language Processing and human action recognition, where capturing longterm dependencies on sequential and temporal data is required. However, their computational structure imposes a challenge when it comes to their efficient mapping on a computing device due to its memory-bounded nature. As recent approaches aim to capture longer dependencies through the utilisation of Hierarchical and Stacked RNN/LSTM models, i.e. models that utilise multiple LSTM models for prediction, meeting the desired application latency becomes even more challenging. This paper addresses the problem of mapping multiple LSTM models to a device by introducing a framework that alters their computational structure opening opportunities for co-optimising the memory requirements to the target architecture. Targeting an FPGA device, the proposed framework achieves \(3\times\) to \(5\times\) improved performance over state-of-the-art approaches for the same accuracy loss, opening the path for the deployment of high-performance systems for Hierarchical and Stacked LSTM models.

Keywords: LSTM, FPGA, Machine Learning, Neural Networks, Singular Value Decomposition, Structured Pruning, High-Performance Computing

Contributions

The proposed framework leverages Singular Value Decomposition (SVD)-based approximation and structured pruning to optimize the execution of multiple LSTMs in parallel. Key components include:

• SVD-Based Weight Approximation: Reduces memory requirements by decomposing weight matrices and selecting a rank-1 representation, minimizing error while improving computational efficiency.
• Structured Pruning: Divides matrices into tiles, pruning low-magnitude tiles to reduce operations and memory access, without requiring retraining.
• FPGA-Specific Accelerator: Implements a custom dataflow architecture on FPGA, featuring dedicated SVD and non-linear kernels to handle LSTM gate computations efficiently.

SVD Approximation Algorithm

The following equation indicates the approximation of a single matrix, i.e., LSTM gate, with \(R\) rank-1 matrices:

Our FPGA accelerator’s leverages the above equation in its key computation. In fact, it approximates vector-matrix multiplication of the \(N\) LSTM inputs with the gate weight matrices, as exemplified in the following equation, which approximates the multiplication between the input vectors \(\textbf{x}_j^t\) with the current forget gates weight matrices \(\textbf{W}_f^{cur}\).

Notice that the vectors \(\textbf{u}^{(i)}_f\) and \(\textbf{v}^{(i)}_f\) are shared accross the \(N\) LSTMs, providing a great compression factor. On top of that, the algorithm also includes a tile-wise pruning scheme to further compress the LSTM weight matrices without impacting their accuracy performance.

The approximation algorithm extracting the SVD components \(\textbf{u}^{(i)}\), \(s^{(i)}_j\) and \(\textbf{v}^{(i)}\) is described in more details in our paper.

HLS Accelerator Architecture

The accelerator architecture is depicted in the following figure:

It comprises several building blocks. It features custom-made DMA engines for streaming in and out models input-outputs and parameters, e.g., weights. The computational engines are instead organized in SVD kernels, which are responsible of executing the SVD-approximated LSTM models.

SVD Kernels Block Diagram

The inner architecture of each SVD kernel is highlighted as follows:

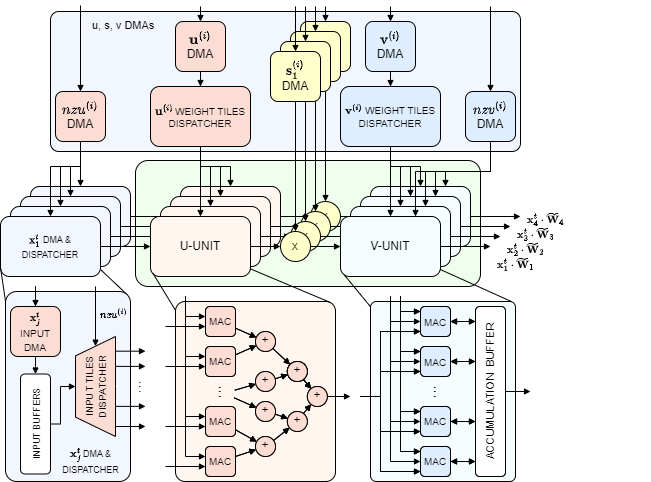
SVD kernels are responsible for the execution of the approximated matrix-vector operation of the LSTM gates mentioned above.

The SVD-kernel is composed of two types of units: U-unit and V-unit. Within the kernel, there are \(N\) U-units and \(N\) V-units. The U-units are responsible for computing the dot product reported in the following equation:

\[ \begin{split} {x_u}_j^{(i)} = \textbf{x}_j^t [{nzu}_k^{(i)}] \cdot \textbf{u}^{(i)} [{nzu}_k^{(i)}],
j = 1, …, N; \quad k = 1, …, T_u - ZT_u \end{split} \]

Each U-unit includes \(T_u - ZT_u\) parallel multiply-accumulate blocks and an adder tree. In order for the U-units to perform their computation, the \(N\) input tiles dispatcher supply the non-pruned input tiles, while the \(\textbf{u}^{(i)}\) tile dispatcher broadcasts the non-pruned tiles. Thanks to the list of indexes \(nzu\) the \(N\) input tiles dispatchers read the input tiles corresponding to the non-pruned tiles of \(\textbf{u}^{(i)}\) and then stream them from their on-chip buffers to the respective MACs within the corresponding U-unit.

The \(N \times R\) scalars \({x_u}_j^{(i)}\) produced by the U-units are then multiplied by the \(s_1^{(i)}, ..., s_j^{(i)}\) scalar components and forwarded to the kernel’s V-units as \({x_s}_j^{(i)}\). The V-units perform the operations in the following equation, i.e., the last step of the approximation process:

Like for the U-units, there is a weight dispatcher which is in charge of supplying the V-unit’s MACs with the non-pruned \(\textbf{v}^{(i)}\) vector tiles. In order to multiply and accumulate the \(x_{s_j}^{(i)}\) scalars with the non-pruned \(\textbf{v}^{(i)}\) weight elements, each V-unit utilizes a partitioned accumulation buffer. The buffer is partitioned tile-wise to allow parallel access to it from the MACs.

Finally, the results of the SVD-kernels are streamed to the \(\sigma\)-kernels for applying the last non-linear functions required by the LSTMs.

Results

We compared our proposed system against two software and two hardware implementations:

• LSTM-SW: Software implementation of baseline LSTM models using GEMV function from OpenBLAS library. Float32 values are used for both activations and weights.
• LSTM-HW: Hardware (FPGA) implementation of baseline LSTM models comprised of 8 parallel 1D systolic arrays for the dense matrix-vector computation, followed by a non-linear unit.
• SVDn-SW: Software implementation of the SVD optimization of the LSTM models that utilizes the same weight values of SVDn-HW before quantization. SVDnSW performs computations on dense weight matrices, despite having many zero values since the OpenBLAS library does not support sparse computation.
• SVD1-HW: A hardware (FPGA) implementation where the mapping of each LSTM model is optimised in isolation.

The baseline implementations without approximation (LSTM-SW and LSTM-HW) are the only ones achieving a 0% accuracy drop. Nevertheless, this is achieved at a high latency, higher than any other design presented. Another expected observation is the fact that all SVDn-SW points have a higher latency than the corresponding SVDn-HW points. The difference observed ranges between a factor of \(3.1\times\) and \(5.6\times\).

Another interesting comparison is between the proposed SVDn-HW and the previously proposed SVD1-HW. In particular, it can be observed that the fastest SVDn-HW design is \(1.7\times\) faster than the fastest SVD1-HW, considering all plotted points have acceptable accuracy. The most accurate SVDn-HW design has \(14\times\) lower accuracy drop than the most accurate SVD1-HW, considering all plotted points have acceptable performance. This is explained by the fact that SVD1-HW applies a similar SVD-based methodology as our approach but does not exploit possible redundancies between weight matrices across LSTM models. As there is a trade-off between accuracy drop and performance, the best SVDn-HW design in the pareto-front is \(2\times\) faster and \(4.5\times\) more accurate than the best SVD1-HW.

Code and Paper Availability

The code for this project is available on GitHub.

An open-access version of the paper can be downloaded here.

Recommended citation: Ribes, S., Trancoso, P., Sourdis, I., Bouganis, C.S., "Mapping Multiple LSTM Models on FPGAs", ICFPT 2020

Link to paper.